FFT(高速フーリエ変換)について
そもそもFFTとは?
FFT はFast Fourie Transform (高速フーリエ変換) の略ですが、実はフーリエ変換ではありません。離散フーリエ変換 (Discrete Fourier Transform, DFT) を計算機上で高速に計算するアルゴリズムです。
厳密に言えば、FFTは「離散的なフーリエ級数展開の係数を高速に求める手法」です。フーリエ級数展開というのは、高調波による時間領域での展開式です。
高速フーリエ変換は、展開式の次数Nが2の累乗のときが最も高速に計算でき、アルゴリズムも単純になることを利用しています。
離散フーリエ係数は、1の原始 N 乗根の1つ \(\small{ WN \equiv exp\left(-2{\pi}i/N\right) }\) を使うと、次のように表せ、これらの要素が対象性を示す(複素共役が存在するなど)ことから高速計算が可能になります。
FFTの結果の単位は?
縦軸のスケール:スペクトル強度
FFT/DFTの結果は、周波数スペクトルの強度になりますが、スペクトル解析の結果をより解釈し易くするため、定数係数を付したり(正規化係数が 1 でない)、エネルギ換算して示す場合があります。
- スペクトルをピーク振幅で表示する場合
- スペクトルを振幅の実効値(RMS)で表示する場合
- スペクトルを計測した結果をパワーで表示する場合
- スペクトルを計測した結果をパワースペクトル密度(PSD)で表示
弊社のモーションレコーダーで用いているスペクトル強度は、①のケースです。
FFT機能について
- グラフの横軸:周波数 単位(Hz)
- グラフの縦軸:パワースペクトル値 単位:(m/sec2/Hz)=(m/sec)
グラフの横軸・縦軸は下記のような形で決まります。
- 周波数の最大値:\(\small{ Fmax = \frac12{\Delta}t (Hz) \quad\text({\Delta}t:サンプリング周期[sec])}\)
サンプリング周期5msec(200Hz)の場合100Hz、1msec(1000Hz)の場合500Hzになります。
- 横軸分解能(周波数分解能):⊿Hz = 1/(2^N * ⊿t)(2^N:データ数)
※ Nは整数。小数点以下は切り捨て。
サンプリング周期1msecでデータ数1000の場合、2^9<1000<2^10なのでFFTで解析できるデータは2^9=512データとなり、上記計算式より⊿Hz=1.9531Hzとなる。
- パワースペクトル値:Sf = 2A/⊿Hz (A:振動振幅)
※ 正弦波での振動、すなわちAsin(ωt+θ)である場合
従って、同じ周波数・同じ振幅の加速度波形であっても、データ計測時のサンプリング周期・FFT解析のデータ数によってスペクトル値は変わります。 比較を行う場合同条件での計測データが必要です。
FFTをすると何が分かるか
FFTを行うと下図のように、横軸に周波数、縦軸にスペクトル強度のグラフが表示されます。そのデータの特徴的な周波数がピークとなってあらわれます。これがFFT波形です。
※下記の画像は『8チャンネル小型無線モーションレコーダ MVP-RF8-HC』(販売終了品)の画面ですが、後継品である『WiFi振動センサー MVP-RF8W-AC』『8チャンネル小型無線モーションレコーダー MVP-RF8-JC』『無線振動データロガー MVP-RF6L-AC』にも同様の解析機能がございます。
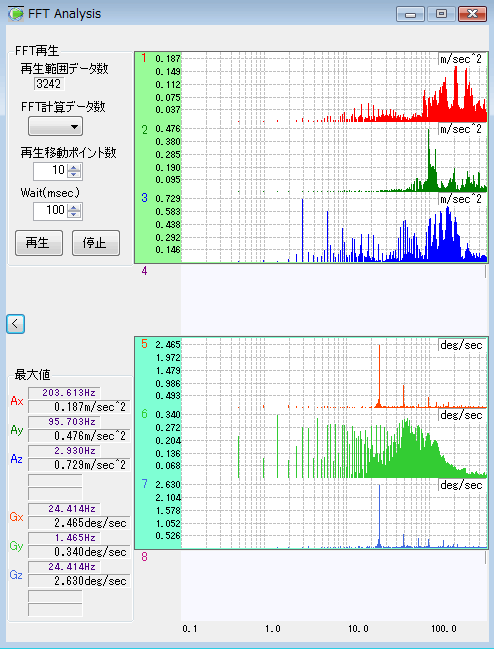
人体計測の場合
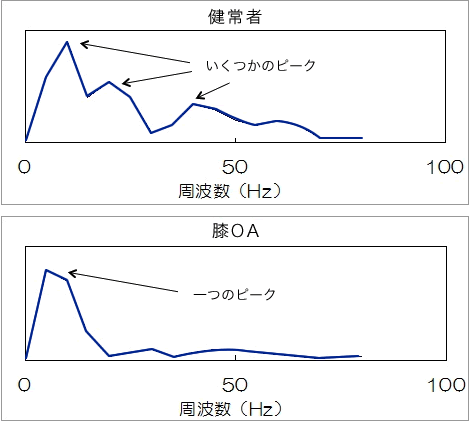
歩行や走行など、繰り返し動作のある動きには特徴的な周波数が含まれます。動きの加速度データをFFTする事により、FFT波形の違いや、特徴的な周波数の違いより、行動の識別ができるようになります。変形性膝関節症など疾病による動きの変化による、周波数的特徴もわかります。
装置計測の場合
正常動作時のFFT波形を確認しておき、その後の計測データによるFFT波形を比較することにより、装置の振動の状況を把握し、故障する前の予防保全のデータとして使用できます。
切削加工など消耗する部品のある加工では、先端の振動を比較することにより、加工のストレスの状態が比較でき、装置による消耗部品の寿命差が推定できます。
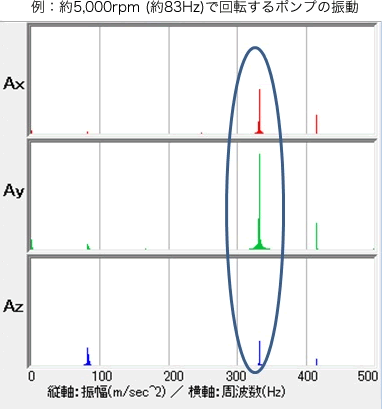
約3倍の周波数に顕著な振動ベアリングなど回転に付随する部品などの影響と推定できる。


